久しぶりに第二種電気工事士の過去問を開くと電圧降下の問題が出てきたので平成25年度上期の電圧降下の問題について解説します。
目次
平成25年度上期の電圧降下の問題で覚えておくべき用語
電圧降下の問題で覚えておくべき用語は
1.電圧降下
2.単相2線式
3.電力損失
の3つです。
まずはこの3つについて解説した後に問題について解説していきます。
※ちなみにこの3つのほかにも内部抵抗や抵抗負荷などが出てきます。
内部抵抗とは電気計器や銅線などに含まれる抵抗を内部抵抗といいます。
そして抵抗負荷とはエアコンやレンジなどに記載している消費電流が抵抗負荷となります。(消費電力が200Wの機械に100Vをかけると消費電流(抵抗負荷)は2Aとなる)
単相2線式とは
「電気の配線の本数は?」と聞かれると大体の人は「2本」と答えるのではないでしょうか?
まさしくその通りです。
この2本で構成された配線を単相2線式といいます。単相2線式は100Vのみに対応しています。
書き方はいろいろありますが、簡単な図にするとこんな感じ
↓

2本の電線のうち1本は接地電線といい、もう1本を非接地電線といいます。
接地電線は大地に接地されているので接地電線という名前になっています。
初めて電気工事士試験を受ける人にとって「大地?、接地?」という感じではないでしょうか?
「大地」は要は地面のことです。「接地」はその名の通りくっついていることです。
上の図でいうとこの部分
↓
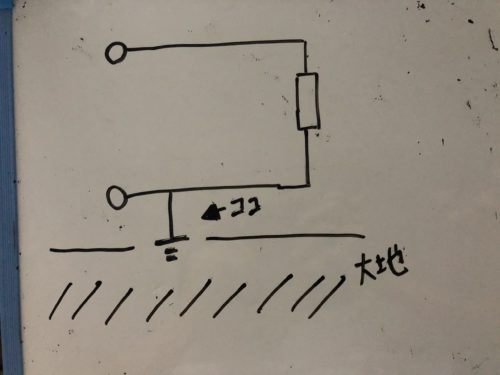
非接地電線はそのまま接地していない電線です。
また、試験では単相2線式は「1Φ2W」と表現されますので覚えておいたほうが良いです。
単相2線式以外にも
・単相3線式(100Vと200Vに対応)
・三相3線式(200Vのみ対応)
などがあります。
電圧降下とは
電圧降下は読んで字のごとく電圧が低く(降下)なることです。
図にするとこんな感じ
↓
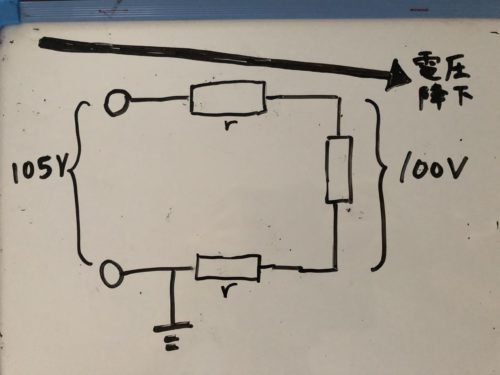
もともと105Vあった電圧が左にある抵抗負荷の範囲をみると100Vになっていて5V分減っています。
これは配線の内部抵抗によって電圧が降下したことになります。
図を見てみると配線は2本ありますね。
1本にある内部抵抗をr(Ω)とすると2本あるので2r(Ω)となります。
そこに負荷抵抗をかけると電流I(A)が流れます。
つまり、オームの法則から降下した電圧量e(V)は
e = 2r × I
となります。
上記の5V分が降下した電圧量です。
電力損失とは
電力損失はその通り電力が損失することです。
これは配線上の内部抵抗r(Ω)によって損失が起こるもので、別名「線路損失」とも呼びます。
電力損失は配線に流れる電流I(A)の2乗に比例します。
よって電力損失Pは
P = 2r × I²
となります。(式の「2」とは配線が2本あるためです。)
平成25年度上期の電圧降下の問題
上記を踏まえて平成25年度上期の電圧降下の問題を解説します。
問題はこれ
↓
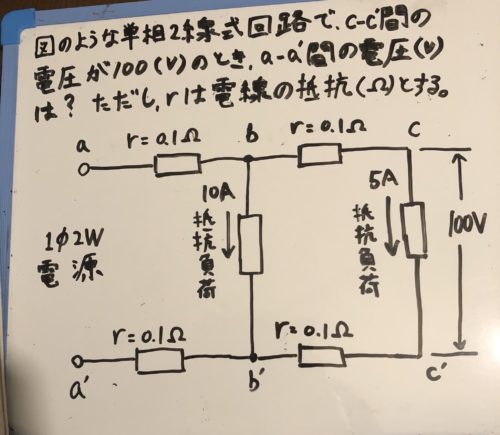
考えるべきは
①a-a間からb-b’間の電圧降下
②b-b’間からc-c’間の電圧降下
の2つを考えます。
①a-a間からb-b’間の電圧降下
ここの内部抵抗は0.1(Ω)となっています。
この内部抵抗を持つ配線が2本あるので0.2(Ω)となります。
次に電流を考えます。
電流は内部抵抗を持つ配線にどのくらいの電流が流れているかがわかれば解くことができます。
まず、b-b’間は10A、そしてc-c’間は5A
これより、電源から出たもともとの電流は
15(A)となります。
よって電圧降下は
e1 = 0.2 × 15
= 3(V)
となります。
②b-b’間からc-c’間の電圧降下
同様にこの間の電圧降下を求めます。
内部抵抗を持つ配線は2本で0.2(Ω)は変わりませんね。
次に電流を考えます。
c-c’間は5Aなので
これより、電圧降下は
e2 = 0.2 × 5
= 1(V)
となります。
この①と②で求めた電圧降下の合計は
e = e1 + e2
= 3(V)+1(V)
=4(V)
となります。
c-c’間の電圧は4(V)の電圧が降下して100Vまで落ちたので
逆をたどるとa-a間の電圧は
104(V)となります。
これがこの問題の答えとなります。