電気に関する勉強を進めていくと「RL直列回路」や「RC直列回路」というものが出てきます。これらは一体なんなのか?解説して行きます。
目次
RL直列回路とは
「RL直列回路」と言われてピンと来にくい方は多いと思います。
まずこのRL直列回路という単語を分解しで説明します。
R:抵抗 L:コイル 直列回路:上記2つを直列に繋いだ回路
これで単語の意味はわかりましたね。
抵抗RとコイルLを直列に繋いだ回路です。
丁寧すぎましたかね^^;
図にするとこんな感じ
↓
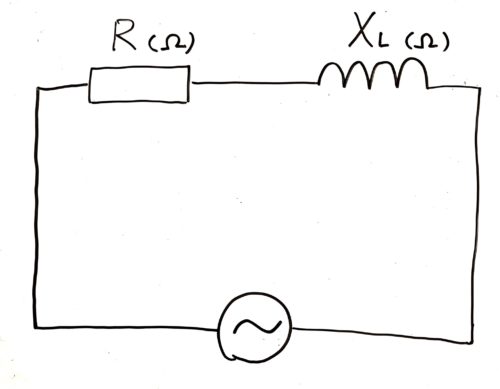
上の図からもわかるように2つとも直列に繋がっていますね。
ここで、このコイルに関してなのですが、このコイルは誘導リアクタンスとも呼ばれています。
誘導リアクタンス = コイル
と覚えてしまいましょう!
誘導リアクタンスはXLという表記で表されます。
抵抗はそのまま抵抗で、Rと表記します。
RL直列回路の「L」はこのXLのLを表していたのです。(Rはそのままですが)
RL直列回路の計算方法
RL直列回路の意味に関しては分かったと思います。
ここからはこの回路の計算方法などを説明して行きます。
もう一度上の図を見てみましょう。
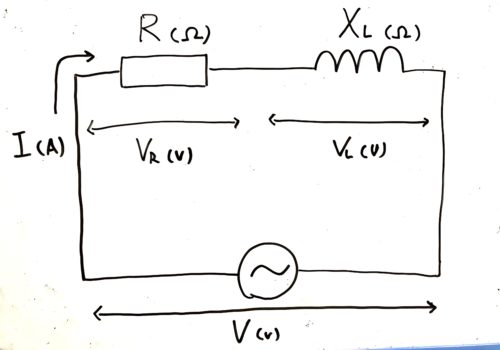
上の図からわかることは電流Iは抵抗Rにも誘導リアクタンスXLにも同じ量流れます。
その他にわかることは抵抗RにはVR(V)分の電圧が誘導リアクタンスXLにはVL(V)分の電圧がかかります。
ここで注意が必要なのは
直列回路だからという理由で
V=VL+VR
という式は成り立ちません。
直列回路でこの足算が成り立つのはどちらも抵抗の場合に足算の式が成り立ちます。
「なら、電圧の求め方はどうやってやるの?」
と思いますよね!
下記でそれを説明して行きます。
ベクトルでの考え方
RLの電圧を考えるにあたり、ベクトルを用いた考え方が必要になってきます、
上記の図からもわかるように抵抗Rにかかる電圧VRには電流Iがかっています。
ここまでをベクトルで表すと以下のようになります。
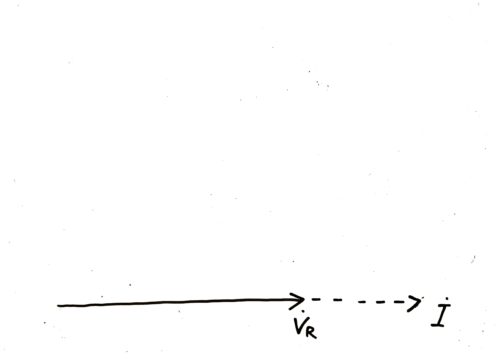
電圧VRと電流Iは同じ向きにありますね。これを同相にあるといいます。
(同相とは位相が同じということです。位相に関してはここでは割愛させていただきます。)
次に電圧VLに関してですが、電圧VLの位相は電流Iよりも90°進みます。
ベクトルで位相が進むことを表す場合は以下のように表します。
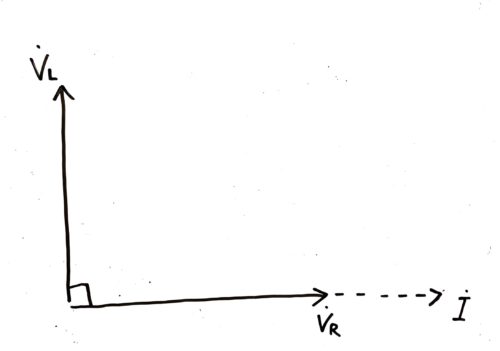
VLが直角に立っていますね。これが電流Iより90°進んでいることになります。
これらを踏まえて全体の電圧は以下のようになります。
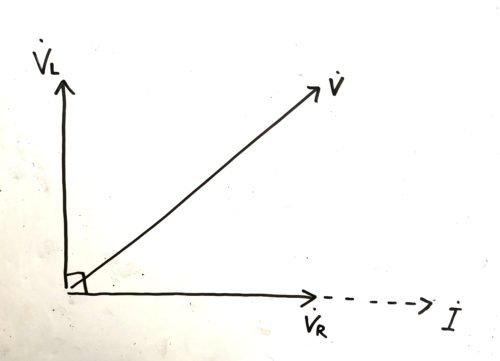
これで全体の電圧VとVLとVRの関係式の条件が揃いました。
これは中学校で習った三平方の定理を用いて解けます。
V=√((VL)^2+(VR)^2)
という式になります。
また、オームの法則より
・VR=I×R
・VL=I×XL
という式が成り立つので、これらを上記に代入すると
V=√((IR)^2+(IXL)^2)
=I√(R^2+XL^2)
となり、全体の電圧が求まります。
このようにベクトルという図で電圧の式を表すことができるのです!
RC直列回路とは
RC直列回路のRは抵抗ですが、
Cはコンデンサのことで、容量リアクタンスといいます。
容量リアクタンス=コンデンサ
図にするとこんな感じ
↓
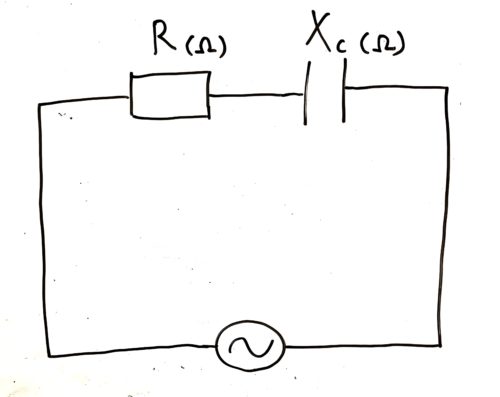
容量リアクタンスはXcという表記で表されます。
電圧の計算方法はRL直列回路と同じように考えます。
電気工事士試験等では必ず出題される範囲なので理解できるようにしましょう!٩( ‘ω’ )و